What Does Horizontal Asymptote Mean
These functions are called rational expressions. As x goes to negative or positive infinity the value of the function approaches a.
 Can A Function Have More Than Two Horizontal Asymptotes Magoosh Blog High School
Can A Function Have More Than Two Horizontal Asymptotes Magoosh Blog High School
For instance f x x 2 1 x 1 does not have a vertical asymptote at x 1 as shown in figure 1 34.

What does horizontal asymptote mean. The function can touch. A horizontal asymptote is not sacred ground however. As the size of x increases to very large values i e.
In other words horizontal asymptotes are different from vertical asymptotes in some fairly significant ways. The function can touch and even cross over the asymptote. That is for a function f x the horizontal asymptote will be equal to lim x f x.
If y ax b is an asymptote of f x then y cax cb is an asymptote of cf x for example f x e x 1 2 has horizontal asymptote y 0 2 2 and no vertical or oblique. Identify horizontal asymptotes while vertical asymptotes describe the behavior of a graph as the output gets very large or very small horizontal asymptotes help describe the behavior of a graph as the input gets very large or very small. If y c is a horizontal asymptote of f x then y c k is a horizontal asymptote of f x k.
It can be expressed by y a where a is some constant. However just because the denominator is 0 at a certain point does not mean there is a vertical asymptote there. There are three types.
Recall that a polynomial s end behavior will mirror that of the leading term. While the denominator does get small near x 1 the numerator gets small too matching the denominator step for step. A horizontal asymptote is a horizontal line that tells you how the function will behave at the very edges of a graph.
An asymptote is a line that a curve approaches as it heads towards infinity. It indicates what actually happens to the curve as the x values get very large or very small. A horizontal asymptote is not sacred ground however.
A horizontal asymptote is simply a straight horizontal line on the graph. The direction can also be negative. In the graphical examples above the curve approaches a constant value b but never actually reaches y 0.
Approaches functions behave in different ways. Horizontal asymptotes exist for functions where both the numerator and denominator are polynomials. Horizontal vertical and oblique.
The curve can approach from any side such as from above or below for a horizontal asymptote. If a known function has an asymptote then the scaling of the function also have an asymptote. A horizontal asymptote is a constant value on a graph which a function approaches but does not actually reach.
A horizontal asymptote is a horizontal line that tells you how the function will behave at the very edges of a graph. Whereas vertical asymptotes indicate very specific behavior on the graph usually close to the origin horizontal asymptotes indicate general behavior usually far off to the sides of the graph. A horizontal asymptote is a fixed value that a function approaches as x becomes very large in either the positive or negative direction.
 Horizontal Asymptotes And Intercepts College Algebra
Horizontal Asymptotes And Intercepts College Algebra
How To Tell If A Function Will Cross The Horizontal Asymptote Quora
 How Do You Find The Horizontal Asymptotes Of A Function Magoosh Blog High School
How Do You Find The Horizontal Asymptotes Of A Function Magoosh Blog High School
 Finding Horizontal Asymptotes Free Math Help
Finding Horizontal Asymptotes Free Math Help
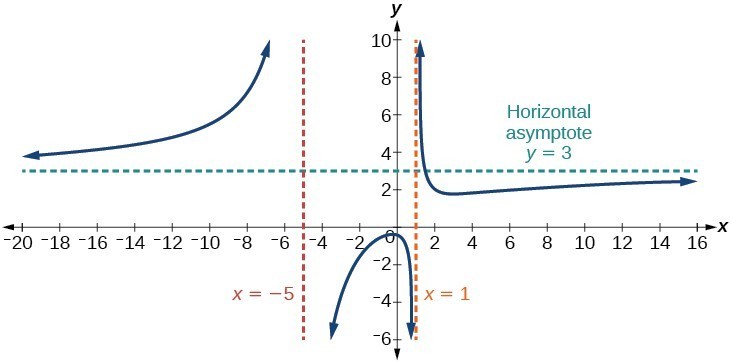 Identify Horizontal Asymptotes College Algebra
Identify Horizontal Asymptotes College Algebra
Math Scene Functions 2 Lesson 3 Rational Functions And Asymptotes
 Do Linear Functions Have Asymptotes Magoosh Blog High School
Do Linear Functions Have Asymptotes Magoosh Blog High School
 Horizontal Asymptote Rules And Defination Share Education
Horizontal Asymptote Rules And Defination Share Education

Post a Comment for "What Does Horizontal Asymptote Mean"